
This webpage by Diane G. Demers explains the orientation congruent algebra and the native exterior calculus of twisted differential forms, provides my draft papers on these concepts, and links some related webpages. We will also discuss polar and axial vectors, as well as ordinary tensors and tensor densities.
The orientation congruent algebra (or OC algebra for short) is a nonassociative, Clifford-like algebra that is essential to the computation of the exterior and Clifford products of twisted multivectors in their natural, or native representation. The resulting two native algebras are called the native exterior algebra and the native Clifford algebra.
Then, just as Cartan's exterior calculus is based on Grassmann's exterior algebra, the native exterior calculus is based on the native exterior algebra which, in turn, is based on the orientation congruent algebra. The native exterior calculus was developed to generalize Élie Cartan's exterior calculus by treating twisted differential forms in their native representation; it is the exterior calculus of twisted differential forms in their native representation.
Here we use the generic term geometric object, or simply object, to refer to both the twisted and untwisted varieties of multivectors, multicovectors, multivector fields, and differential forms, even though this usage may differ from that of differential geometry. Following de Rham, twisted objects are also commonly described as impair (French) or odd (English); while ordinary, untwisted (straight) objects are also commonly described as pair (French) or even (English). On this website we freely interchange the two terms twisted and odd, as well as the two terms straight and even.
To quickly get an intuitive feeling for twisted differential forms see Rob Salgado's richly illustrated conference poster "Visualizing Tensors." For more excellent illustrations of twisted differential forms see also Bill Burke's book and papers, or Schouten's book Tensor Analysis for Physicists, which, however, uses classical tensor analysis notation exclusively.
This framework of the native representation of twisted objects using the orientation congruent algebra applies to manifolds of any finite dimension n. It ends the confusing manual sign choices required by, other, previously known approaches. We will see that, by clearing up the many misunderstandings engendered by the usual techniques, this natural and general formulation for twisted geometric objects powerfully resolves many smoldering controversies that repeatedly appear in the mathematics and physics literature.
The latest example of such a controversy is provided by the following series of papers (the last two of which cite this website and my works):
AdPreply_100107.pdf
For more background related to the statements made in the above submitted paper see the section on the native Clifford product of native brackets.
These controversies about twisted physical quantities, although sometimes couched in powerful abstract formalisms, are all rooted in the simple, prototypical clash of two sets of concepts: unoriented and twisted space vs. oriented vectors.
Our first natural conception of space is, both in physics as well as everyday life and commerce, unoriented. For example, one would not, I think, approach an appliance salesperson and ask to see some refrigerators having a capacity of "546 liters with a right-hand screw sense," rather than simply "546 liters." However, it is meaningful to assign a positive or negative sign to capacity so that gains and losses in volume may be accounted; therefore space may be also be naturally considered as being oriented as an odd or twisted trivector (also called a three-vector or 3-vector).
On the other hand, vectors and their higher grade analogs, such as bivectors and trivectors, are all patently oriented (in the common sense). They are thus examples of what we call even or straight vectors, bivectors, and trivectors.
(The above discussion suggests the tangential question of whether perhaps extremely precise measurements will someday reveal that the volume of a stationary or moving cube determined by measurements taken in the order of, say, height, width, and then depth is different from its volume determined by measurements taken in a different order.)
To Be Developed Further
The axioms for geometric (Clifford) algebra that Hestenes and Sobczyk give in their book Clifford Algebra to Geometric Calculus were apparently constructed to be directly analogous to those for the real numbers (perhaps, in part, to entice physicists into studying them). We may also recall that there is a long tradition of calling the elements of Clifford algebras Clifford numbers. (Similarly, we have the terms complex numbers, double numbers, and, generally, hypercomplex numbers.)
The next step is to extend the current conception of geometric (Clifford) numbers by considering how sign fits into this analogy. That is, we have in the geometric (Clifford) numbers a geometric generalization of the real numbers, but only the most primitive generalization of signed real numbers: namely, that in which the geometric sign has the same attitude as (this phrase is explained shortly below, but for now it may be roughly read as is parallel with) the geometric "absolute value" or magnitude.
By entertaining the further possibility that the geometric sign of a geometric number may be transverse (in a nonmetric setting) or orthogonally complementary (in a metric setting) to its geometric magnitude we obtain the twisted multivectors. These twisted geometric numbers have both mathematical and physical implications. And this new theory of the native representation of twisted geometric objects provides an adequate foundation for the investigation of those implications.

The Finest Geometric Decomposition of a Vector The figure above illustrates the finest geometric, basis-independent and nonmetric decomposition of a nonzero vector b. This decomposition consists of a line l, a line segment s, and a ray r. The ray r is drawn with a double arrowhead to distinguish it from the vector b. The equal and addition signs are metaphorical.
b = [[λe1, e1]].And we may call the vector λe1 for some λ > 0 a ray representative of the native geometric sign equivalence class.
Gsnn b = {v | b = [[v, e1]]}.Then we then obtain
λe1 ∈ Gsnn b, for all λ > 0,or, equivalently,
{λe1 | λ > 0} ⊂ Gsnn b.However, we note that
Gsnn b ≠ {λe1 | λ > 0}.The last inequality is true because the ray described by λe1 is not large enough to include all elements of the equivalence class that is Gsnn b. However, we give next an expression for the complete native gsign equivalence class.
Gsnn b = {λe1 + u | for all λ > 0 and all u ≠ μb for some μ}.And this imples that
b = [[λe1 + u, e1]], for all λ > 0 and all u ≠ μb for some μ.
Gsnn b = {v | v ≠ λe1 for some λ ≤ 0} = V \ {λe1 | for all λ ≤ 0}.
Then also, following the alternative sense of the word ray introduced just above, we may say that the set described by the expression λe1 + u in the gsign position above is the (nonpositive) ray-deleted space associated with b. (We must say "nonpositive" here because the zero vector is also removed.) However, rather than this straightforward but cumbersome phrase, let us call this set of rays a fan since, if it is associated with a vector in a 2-dimensional enveloping vector space, its appearance suggests a hypothetical hand-held oriental folding fan that has been opened to an almost 360° circular sector. Note that this definition of a fan is applicable to any nonzero even, simple (decomposable) multivector of any grade in an enveloping vector space of any dimension.
Gsnn −b = {−(λe1 + u) | for all λ > 0 and all u ≠ μb for some μ},which imples that
−b = [[−(λe1 + u), e1]], for all λ > 0 and all u ≠ μb for some μ.We also have, more generally, for any (even or odd) simple (decomposable) multivector b
Gsnn −b = −Gsnn b,if we make the natural interpretation that the negative sign on the right-hand side distributes over all elements in the equivalence class.
Gaun b = {v | b = [[e1, v]]}.Recall now that the gauge of b is geometrically represented as a line segment of the same length parallel to it. This implies that the algebraic sign of the gauge is irrelevant. Then we have
b = [[e1, ±e1]].Then we obtain simply
Gaun b = {±e1}.We also have, more generally, for any (even or odd) simple (decomposable) multivector b
Gaun b = Gaun −b = −Gaun b,if we make the natural interpretation that the negative sign in the rightmost expression distributes over all elements in the equivalence class.
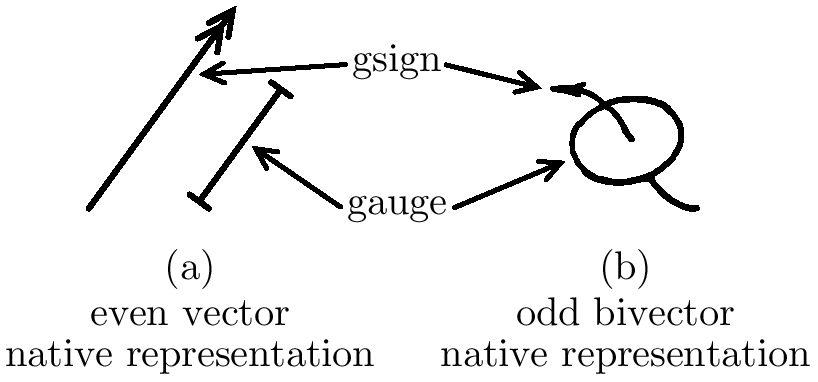
is used to represent one of the oriented vector subspaces in the equivalence class of those associated with the gsigns in the native and correlated representationsThe Geometric Pictures of (a) an Even Vector and (b) an Odd Bivector in the Native Representation The figure above shows side-by-side the geometric pictures of a nonzero even vector b and a nonzero odd bivector C. The ray representing the gsign of b is drawn with a double arrowhead in conformance with the previous figure. However, the image of the odd bivector in this figure is adapted from Schouten's book Tensor Analysis for Physicists, in which he draws the ray representing its gsign as a curvy arrow with a single arrowhead. The curviness of this arrow may be interpretated as an indication that it actually represents one of the oriented vector subspaces in the equivalence class of those associated with the gsign of the odd bivector.
UNDER REVISION
UNDER REVISION
The native representation of a twisted bivector can also be written in bracket notation. For example, let the twisted bivector C be [[e1, e23]].
UNDER REVISION
The native representation of a twisted bivector can also be written in bracket notation. As a specific example, let the twisted bivector C = [[e1, e23]], where e1 and e23 are basis multivectors. Since the gsign of C may be geometrically represented as a ray parallel to e1, any positive multiple of e1 may occupy the gsign position in the native bracket. And thus we have for all real numbers λ > 0
C = [[λe1, e23]].However, we also have the inequality
gsnn C ≠ λe1because the ray described by λe1 is not large enough to include all elements of the equivalence class that is the native gsign of C.
UNDER REVISION
We may now make one critical addition to the above equation to reflect the fact that the geometric sign actually represents an even larger equivalence class of oriented subspaces than that described by its ray representative, λe1. As was true for an even vector, the oriented subspace that is gsnn C may also be interpreted as an element of an oriented projective space. However, now this element must be transverse to or not incident with the basis multivector in the gauge position of the native bracket for C, that is e23. Under this interpretation the gsign must be invariant under all oriented projective transformations (see
Stolfi's book).
Thus, we have for all vectors u such that u ∧ e23 = λ e1 ∧ e23 for some λ > 0
C = [[u, e23]].In the expression λe1 + u appearing above in the gsign position, the term λe1 represents one of the oriented vector subspaces in the equivalence class of those associated with this gsign. The set of all oriented subspaces in this equivalence class is, of course, represented by the full gsign expression.
In our case, it is the native representation that is used to multiply both even and odd objects, while the correlated representation is used to add, multiply, and differentiate them. This last use is most important since we aim to construct a caculus. And, just as one would not dream of using the polar form to do complex analysis, so too we must use the correlated representation to do the native exterior calculus.
Finally, to connect with the usual differential geometry notation for odd differential forms we need one more representation, the extremum. The extremum representation is so named because its first component's grade is always either the smallest possible grade grade 0, or the largest possible grade n. That is, the first component of the extremum representation is always an arbitrary non-zero scalar multiple of either 1 or Ω±. For an explanation of the meaning and significance of the symbols Ω± and Ω+ used here and throughout this website, please see the section on the two types of OC algebras.
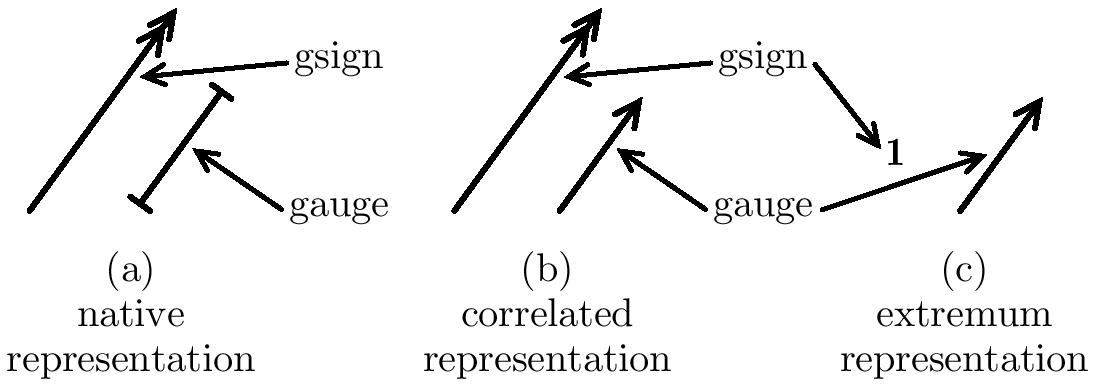
The Geometric Pictures of an Even Vector in the (a) Native, (b) Correlated, and (c) Extremum Representations The figure above shows side-by-side the geometric pictures of a nonzero even vector b in the native, correlated, and extremum representations. In this figure a doubleheaded arrow is used to represent one of the oriented vector subspaces in the equivalence class of those associated with the gsigns in the native and correlated representations. This is a different convention than that used by Schouten in his book Tensor Analysis for Physicists.
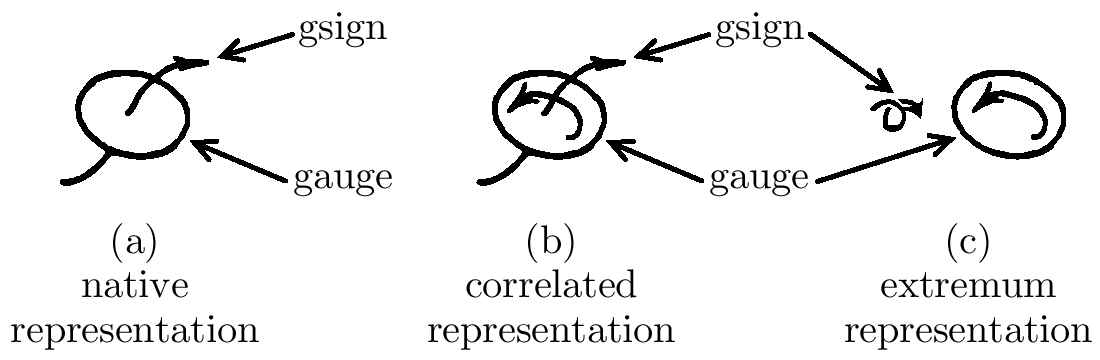
The Geometric Pictures of an Odd Bivector in the (a) Native, (b) Correlated, and (c) Extremum Representations The figure above shows side-by-side the geometric pictures of a nonzero odd bivector C in the native, correlated, and extremum representations. The above image of an odd bivector in the native representation is adapted from Schouten's book Tensor Analysis for Physicists.
The symbols for these three representations consist of ordered pairs that are written within doubled brackets. As suggested by this notation, these three representations will henceforth generally be called the native, correlated, and extremum brackets (rather than representations). They are given in the following table along with some odd and even examples of each. These examples are all from a manifold or space of dimension 3. The first component of all three brackets in this table is the gsign, written generically as s; the second component is the gauge, written generically as g.
| Type | Symbol | Examples | |
|---|---|---|---|
| Odd | Even | ||
| Native | [[sn, gn]] | [[e1, e23]] | [[e1, e1]] |
| Correlated | <<sc, gc>> | <<e1, e23>> | <<e1, e1>> |
| Extremum | ((se, ge)) | ((Ω+, e23)) | ((1, e1)) |
| Type | Native | Correlated | Extremum |
|---|---|---|---|
| Migratory | −[[sn, gn]] = [[−sn, −gn]] | −<<sc, gc>> = <<−sc, −gc>> | −((se, ge)) = ((se, −ge)) |
| Unbinding | [[sn, gn]] = [[sn, −gn]] | — | ((se, ge)) = ((−se, −ge)) |
The symbolic correlated and extremum representations of geometric objects were originally presented on this webpage in a text file that I continue to include here for historical purposes: NatRep.txt. As is evident, the terminology and square bracket notation used in this file has been changed to that used above in the current version of this webpage and also in the draft paper on the native exterior calculus.
In the native representation the definitions of both the Clifford and exterior products of multivectors are almost trivial (although perhaps conceptually challenging to those accustomed to the standard formalisms). In light of this near triviality, one may ask why should we bother to express these operations in the correlated representation? The answer is that the process of exterior differentiation requires the simultaneous use of multiplication and addition. And, since the addition of multivectors is most naturally expressed in the correlated representation, we must work in the "lowest common denominator"—the correlated representation—when we take derivatives.
To Be Developed Further
The Native Clifford Product of Native Brackets. We now provide the almost trivial definition of the native Clifford product for multivectors in the native representation. Let u and v, respectively, be twisted or straight simple (decomposable) multivectors with representations in native brackets given by [[su, gu]] and [[sv, gv]], respectively. Then the native Clifford product of u and v is defined as
u õ v := [[su @ sv, gu @ gv]].Here we have symbolized the native Clifford product as õ, lower case o with tilde (an HTML substitute for my preferred symbol the AMS LaTeX operator \tilde{\circ}), and the orientation congruent product as @, the "at sign." We have also used s and g, respectively, as generic symbols for the gsign and gauge, respectively, of a native bracket.
Note that the native Clifford product is inherently nonassociative since the sign-determining multiplication of the gsigns is effected by the nonassociative orientation congruent product. We are, in fact, forced to adopt this surprising definition to maintain consistency with the rest of the native representation and algebra framework. Also note that the product of the gauges may also be computed with the ordinary Clifford product (or any other Clifford-like product) rather than the OC product since the sign of a native bracket's gauge is irrelevant.
For those practitioners of the more or less standard Clifford algebra-based theories, such as Hestenes and Sobczyk's geometric calculus of multivectors or Rodrigues and Capelas de Oliveira's Clifford bundle approach, the inherent nonassociativity of the native Clifford product may present a challenging shock. It implies that the set of physically meaningful equations expressed in these formalisms includes only those that can be reformulated into an equivalent native Clifford algebra version. This statement may be dubbed the principle of nonassociative irrelevance, or, perhaps, algebraic indifference. The native Clifford algebra also seems to be the first nonassociative algebra that is naturally and widely applicable to many areas of physics. For related commentary see my paper submitted to Annalen der Physik (Berlin).
To Be Developed Further
I am currently writing a paper on the native exterior calculus of twisted differential forms. As mentioned above in the introduction to this webpage, the orientation congruent algebra is integral to developing the native exterior calculus. This paper, "Exterior Calculus in the Image of Odd Forms with the Orientation Congruent Algebra," will treat two problems in electrodynamics as examples.
An abstract of this draft paper: ExtCalc.pdf.
To Be Added
In this section I present as much information as possible about the orientation congruent algebra. It should become clear to the reader of this section that this algebra has a life of its own outside of its application to the native representation of twisted geometric objects.
This section also needs more work. For the moment, we simply state that the author's initial motivating application of the orientation congruent algebra was to directly calculate the exterior product of straight and twisted multivectors in their native representation. This required the development of the native exterior algebra which, in turn, is the algebraic basis of the native exterior calculus.
Properties of the OC algebra include the following:
The orientation congruent algebras naturally divide into two classes depending on the commutation properties of the unit-magnitude, maximum-grade multivector. This division is exactly mirrored by the parity of the underlying vector space of grade 1 multivectors, or base space. The unit-magnitude, maximum-grade multivector of an OC algebra with an odd-dimensional base space commutes with all other multivectors just as the identity or unit element 1 does. On the other hand, the unit-magnitude, maximum-grade multivector of an OC algebra with an even-dimensional base space does not possess this propery.
In both types of orientation congruent algebras the unit-magnitude, maximum-grade multivector has a grade which is complementary to that of the unit element since n + 0 = n. And so we call it a counit. For OC algebras with an odd-dimensional base space we call it a perfect counit, while for OC algebras with an even-dimensional base space we call it an imperfect counit. An orientation congruent algebra with a perfect (resp., imperfect) counit is called a perfect (resp., imperfect) OC algebra.
These facts are reflected by the multiplication tables presented in the section below: The most symmetrical multiplication tables are those for which the OC algebras have odd-dimensional base spaces and perfect counits.
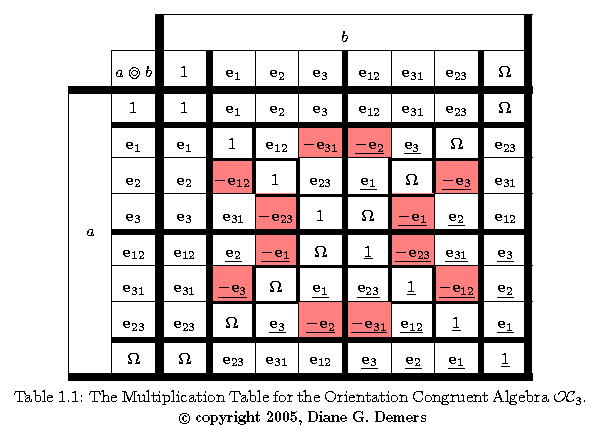
In these tables the perfect counit for those orientation congruent algebras with an odd-dimensional base space is represented by the symbol bold capital Omega Ω (similar to differential geometry's usage). Thus the bold capital Omega in the table for OC3 is equal to e123 while that in the table for OC5 is equal to e12345. On the other hand, the imperfect counit for those orientation congruent algebras with an even-dimensional base space is represented by the symbol upside-down bold capital Omega ℧ (\mho in AMS LaTeX). Thus the inverted bold Omega in the table for OC4 is equal to e1234. An inverted bold Omega is used to alert the reader that, as explained just above, the counit in OC algebras with an even-dimensional base space, unlike the odd-dimensional case, is imperfect, and so does not generally commute with other multivectors under OC multiplication.
In contrast to these tables (for which the niceties of LaTeX typography are available) in the text of this webpage (and perhaps also on the blackboard) we modify the above conventions for counit symbols. Thus we also use the symbol bold capital Omega with a plus sign subscript Ω+ for the perfect counit of an orientation congruent algebra with an odd-dimensional base space but a not necessarily specified dimension or signature. On the other hand, we use the symbol bold capital Omega with a negative sign subscript Ω− for the imperfect counit of an orientation congruent algebra with an even-dimensional base space but a not necessarily specified dimension or signature.
Here we also introduce the term indefinite counit for the counit of an OC algebra with both a not necessarily specified base space parity and a not necessarily specified signature. In LaTeX documents we indicate an indefinite counit with a symbol that is a stylized version a superimposed noninverted and inverted bold Omega. However, in the text of this webpage we indicate an indefinite counit with the symbol bold capital Omega with a "plus or minus sign" subscript Ω±.
The most direct understanding of an algebra is obtained by studying its multiplication table. By multiplication table we mean, more formally, the partial Cayley table of the group induced by an associative algebra, or the partial Latin square of the quasigroup induced by a nonassociative algebra. These tables are partial in that they contain only products whose factors have a positive sign in some standard representation.
We next present the multiplication tables of three OC algebras that are particularly important in our exposition. Note that in the multiplication tables (displayed or downloadable below) for the orientation congruent algebras OC3 and OC5, but not OC4, the products which have a sign which is opposite to that of the corresponding Clifford algebra products have been underlined. Also note that some symmetries of these tables have been made more visible by tinting red the cells which contain negative entries.
For an explanation of the meaning and significance of the two symbols in these tables, bold capital Omega Ω and upside-down bold capital Omega ℧, please see the above section on the two types of OC algebras.
The multiplication table for the orientation congruent algebra OC3 (or OC3,0) displayed as a PNG graphic:
The multiplication table for the orientation congruent algebra OC4 (or OC4,0) downloadable as an Adobe Acrobat PDF file (22,652 bytes), January 3, 2010: OC40MultTab1-2.pdf
The multiplication table for the orientation congruent algebra OC5 (or OC5,0) downloadable as an Adobe Acrobat PDF file (49,525 bytes), June 23, 2005: OC50MultTab1-3.pdf
The orientation congruent algebra is a Clifford-like algebra. Clifford-likeness, in the sense that I use this term, may be defined by considering products of the basis multivectors that are derived from an orthonormal set of basis vectors. Then the Clifford-likeness of some algebra means that the product of two given basis multivectors in that algebra is same as their Clifford product up to a ± difference in sign. In other words, the OC product is a ± sign deformation (or mutation) of the Clifford product.
The orientation congruent algebra is a member of the large class of nonassociative algebras known as noncommutative Jordan algebras. I have proved this by a brute force case-by-case examination using Wolfram Research's Mathematica software. Although the code executes in a reasonable time, it would be good to have an analytical proof. The Mathematica code and its explanation are available upon request.
Although I have not yet written up my notes for a proof of this fact, the formulas for the Hodge star dual operator and its inverse are
* α = (Ω±)−1 @ α, andHere lower case alpha α is an arbitrary straight (not twisted) differential form in its ordinary (not native) representation, bold capital Omega with a plus or minus sign subscript Ω± is the volume form, and the at sign @ is the OC product. (The at sign @ is an ASCII substitute for the symbol that I prefer, the AMS LaTeX \circledcirc or the Unicode character "CIRCLED RING OPERATOR" U+229A which may be coded as "⊚" in HTML but which is not properly displayed by all web browsers.) The inverse of the volume form Ω±, written above as (Ω±)−1, is with respect to the OC product.
*−1 α = α @ Ω±.
Here we have used the symbol convention laid down in the above section on the two types of OC algebras to represent the volume form by a bold capital Omega with a plus or minus sign subscript Ω±. Distinguishing between a perfect and imperfect counit, respectively, by following our convention of using a bold capital Omega with a plus sign subscript Ω+ and one with a negative sign subscript Ω−, respectively, is not necessary in these formulas since they are generally valid for both odd- and even-dimensional manifolds.
These formulas are also valid for both Riemannian and pseudo-Riemannian metrics. Note, however, that for pseudo-Riemannian metrics the formulas for the Hodge star and its inverse may need to be interchanged depending on which of the two possible conventions is observed. Furthermore, these formulas may be rather trivally extended to twisted differential forms represented either in the standard notation of differential geometry or in the equivalent extremum bracket notation of the native framework.
It is certainly possible (and worthwhile) to express the orientation-invariant Hodge star operator and its inverse (just as naturally as in the above formulas) using either the standard differential geometry representation for twisted forms or the equivalent bracket representations. However, we reserve this exercise for another time.
On page 750 of the Grassmann Algebra book is the citation:
Hodge W V D 1952
Theory and Applications of Harmonic Integrals
Cambridge
The "star" operator defined by Hodge is of similar nature to Grassmann's complement operator.
And on page 341 Browne makes this allusion:
In more modern works the Ergänzung for general metrics has become known as the Hodge Star operator. But we do not use the term here since our aim is to develop the concept by showing how it can be built straightforwardly on the foundations laid by Grassmann.
Along this line we also provide this quotation from page 7, section 6, "Grassmann-Hodge stars (Kocik 1979)," of the paper "Isometry from reflections versus isometry from bivector" by Zbigniew Oziewicz (2009, Online First, Adv. Appl. Clifford Alg.):
The concept of a ‘Hodge-star’ was introduced by Hermann Grassmann in his second monograph in 1862, under the name ‘Ergänzung’ (supplement) [Grassmann 1862, § 3.4 ]. The present-day star-notation, *, was introduced by Hermann Weyl in 1945.
Based on this precedence I suppose then that one could call the orientation congruent algebra the Clifford-Grassmann algebra (or CG algebra for short). But that is perhaps too confusing given current terminology. The possibility is also raised that the full orientation congruent algebra is also cryptically or, at least, implicitly contained in Grassmann's work.
The OC2 algebra is isomorphic to the hyperbolic quaternions of Alexander Macfarlane. Macfarlane published a paper "Hyperbolic Quaternions" (1989-1900, Proc. Royal Society of Edinburgh 23:169-181) on his discovery of "a system of quaternions complementary to that of Hamilton, which is capable of expressing trigonometry on the surface of the equilateral hyperboloids."
According to this brief biographical essay on Macfarlane, Emil Borel later observed that the 3D hyperboloid model of hyperbolic space describes the kinematic velocity space of special relativity. Also see the webpage "Alexander Macfarlane and the Ring of Hyperbolic Quaternions" and the Wikipedia webpage "Hyperbolic quaternion."
The series of orientation congruent algebras OCn starting with n = 1 and increasing are isomorphic to the the double or split-complex numbers for n = 1, the hyperbolic quaternions for n = 2, and their generalizations to higher dimensions for n > 2. These generalizations are part of the sequence of structurally-hyperbolic Cayley-Dickson algebras that are dual in a natural sense to the usual Cayley-Dickson algebras, which may then be called structurally-elliptic. See the section on the structurally-hyperbolic algebras.
Title:
The Orientation Congruent Algebra: A Nonassociative Clifford-Like Algebra
Abstract.
The correlated grade form of twisted blades (twisted simple multivectors)
faithfully renders in symbols their native geometric structure. The discovery
of this paper's nonassociative Clifford-like algebra was driven by trying to calculate exterior products of straight and twisted multivectors directly in a basis of
this form. The key was found to be the orientation congruent (OC) algebra. This
paper is being published electronically in about ten sections, each offered as soon
as written. In this first section we axiomatize the orientation congruent algebra
by generators and relations. The next section derives the sign factor function sigma and proves that the Clifford product times it is the multiplication of an explicitly Clifford-like algebra isomorphic to the orientation congruent algebra. Later sections are planned to show how to calculate the OC product in Mathematica and Clical; to define the orientation congruent contraction operators, deduce their properties, derive other expressions for them, and use them to compute the OC product within the exterior algebra using a modified Cartan decomposition formula; to develop the algebra's product sequence graph with labeled edges; to derive a predictor of a null associator as a function of the grades of the three elements in it; to prove the associomediative property of the algebra's counit; to develop matrix representations (under a nonassociative matrix product) of the orientation congruent product; and to discuss the motivating application per se and as inspiration for the first set of axioms.
This paper is available for downloading or reading online. It will be split by section into separate PDF files. Each file will be offered as soon as it is written. As the paper approaches completion the finished sections may be combined into one file. Revisions may occur so be sure to get the latest versions of each section.
Section 1: An Axiom System for the OC Algebra
Version 1.3, June 27, 2005: Adobe Acrobat PDF file (295,623 bytes),
OriCon013ch01.pdf
Note: Contrary to the above plan, this paper will not be posted section-by-section and may possibly not be developed further beyond version 1.5 below. But some essential material from this paper will incorporated into the newer paper on the native exterior calculus
Title:
The Orientation Congruent Algebra
Part I: A Nonassociative Clifford-Like Algebra
Abstract. Similar to Version 1.3.
Table of Contents
Complete paper: The Orientation Congruent Algebra: A Nonassociative Clifford-Like Algebra
Version 1.5, December 4, 2005: Adobe Acrobat PDF file (865,403 bytes),
OriCon015ch01-09.pdf
Note: There are few errors in this draft; but none of them is fatal to the thrust of this research. An errata sheet or a revised draft paper will eventually be posted here.
This section added rather hastily on December 9, 2009 puts the cart before the horse since the fundamental sections on the native Clifford and native exterior algebras are currently empty. However, my research has picked up dramatically in the last 2-3 months. And although at present this work resides only in my notes and memory, I will here describe some more recent investigations.
I now know how to use the orientation congruent algebra in even-dimensional spaces—which has been a problem since the beginning many years ago. It requires in part using a "nonmetric" approach.
I put quotation marks around the word nonmetric above because in this approach we apply a peculiar kind of Clifford algebra (or, actually, its related orientation congruent algebra) which may be called variously a nonmetric Clifford algebra, or a formally metric Clifford algebra or, using perhaps the best choice of words, a Clifford algebra of multivecfors (please note, not multivectors) following the terminology of the paper by W. A. Rodrigues, Jr. and Q. A. G. de Souza at http://arxiv.org/abs/math-ph/0703053.
This type of Clifford algebra has also been developed for manifolds using a bundle-theoretic approach by M. P. Burlakov in the very last section of his paper "Clifford structures on manifolds." The original Russian version is at http://mi.mathnet.ru/eng/into27 and an English translation is at http://dx.doi.org/10.1007/BF02414874.
Reviews are at http://www.ams.org/mathscinet-getitem?mr=1619716 and http://www.zentralblatt-math.org/zmath/en/search/?q=an:0930.53030&format=complete.
In addition, a further interesting complication is that while odd-dimensional spaces require the orientation congruent algebra derived from the (rather more standard) orthogonal version of the Clifford algebra of multivecfors (that is, with the split-Euclidean metric of signature (n, n), for an n-dimensional space), on the other hand, the even-dimensional spaces require a Clifford algebra of an arbitrary, nonsymmetric bilinear form in the terminology of Bertfried Fauser and Rafal Ablamowicz in http://arxiv.org/abs/math.QA/9911180
This is also known as a quantum Clifford algebra to use the terminology of Bertfried Fauser in http://arxiv.org/abs/math.QA/0202059
See also Rafal Ablamowicz and Pertti Lounesto's book chapter "On Clifford algebras of a bilinear form with an antisymmetric part" at http://books.google.com/books?id=OpbY_abijtwC&pg=PA167
I have seen the need to use this generalized type of Clifford algebra several times over the years. However, that was still within a metrical context. And then the bilinear form involved was truly a generally nonsymmetric bilinear form, that is, neither purely symmetric nor antisymmetric. However, the situation is much simplified by using the nonmetric Clifford algebra of multivecfors which combines the space of multivectors with the dual space of multicovectors into one space.
Then the nonsymmetric bilinear form involved is not so arbitrary, but is properly the symplectic bilinear form associated with a symplectic vector space. For an n-dimensional physical space this symplectic vector space requires a 2n-dimensional (Wick) basis of vectors and covectors. Then, for example, the matrix representation of the symplectic bilinear form for a 2-dimensional physical space may be written in the standard form
[ 0 1 0 0 ] [ -1 0 0 0 ] [ 0 0 0 1 ] [ 0 0 -1 0 ].
Then it is the case that for an even-dimensional physical space (e.g., 4-dimensional spacetime), the final algebra that is used is the orientation congruent analog of the Clifford algebra of multivecfors, which, in turn, is the analog of the Clifford algebra of a symplectic bilinear form.
Also, apparently, the Clifford algebra of multivecfors can be nicely explained in the abstract language of mathematical category theory and it appears to be based on the biproduct of a module. See the books reviewed at http://www.ams.org/mathscinet-getitem?mr=941522 and http://www.ams.org/mathscinet-getitem?mr=1712872.
I could go further here and tie the notion of a correlation in projective geometry into this phenomenon that odd- and even-dimensional spaces, respectively, must be treated by algebras associated with bilinear forms that are either split-Euclidean or canonically symplectic, respectively. However, I will only add that these new concepts create a naturally nonmetrical setting for projective geometry. They then provide a true nonmetrical foundation for projective geometry which the cobasis used by John Browne in his Grassmann Algebra book does not.
I also think that implied in this new work may be a foundation for Hestenes and Sobczyk's geometric calculus of multivectors. But that is a long-term project. I am now busy writing up this new material and integrating it with my earlier results.
As mentioned in the above section on the properties of the OC algebra, the orientation congruent algebra may be viewed as a structurally-hyperbolic Clifford algebra, a generalization of the usual Clifford algebra. That is because the foundation of the orientation congruent algebra lies within the new algebraic theory of structurally-elliptic and structurally-hyperbolic algebras.
In this framework, the usual Clifford algebra, which we call structurally-elliptic, is the dual of the orientation congruent algebra, which we call structurally-hyperbolic. This terminology has its origin in the fact that the Clifford algebras are naturally suited to represent elliptic (ordinary) rotations in the prototypical spaces with Euclidean signature (n, 0) while the orientation congruent algebras are naturally suited to represent hyperbolic rotations (boosts) in the prototypical spaces with Lorentzian signature (n-1, 1). More about this will be added later.
This Clifford algebra dualization leads naturally to the dualization of the structurally-elliptic Cayley-Dickson algebras (i.e., the usual Cayley-Dickson algebras) to the structurally-hyperbolic Cayley-Dickson algebras. These new algebras are partly illustrated in the section on Macfarlane's hyperbolic quaternions (which we may more systematically call the structurally-hyperbolic quaternions).
The loops (quasigroups with identity) induced by the structurally-hyperbolic Cayley-Dickson algebras are characterized by some interesting new identities. In particular, it turns out that the structurally-hyperbolic octonions are neither Bol nor Moufang loops, but a kind of hybrid of the two. More details on this will be forthcoming as time permits.
"Structurally-Hyperbolic Algebras Dual to the Cayley-Dickson and Clifford Algebras or Nested Snakes Bite Their Tails" is the title of a draft paper on this theory. The unusual subtitle is an allusion to an exclamation written into an early paper by the knot theorist Louis H. Kauffman. A particular formula in that early paper of Kauffman inspired a more general formula for the product of the structurally-hyperbolic Cayley-Dickson algebras. In fact, this draft paper mostly establishes basic terminology and the fundamental formulas relating the two kinds of Cayley-Dickson algebra products—structurally-elliptic and structurally-hyperbolic.
An abstract of this draft paper:
Nested_080715_abs.pdf.
The latest draft of this paper from July 15, 2008:
Nested_080715.pdf.
This webpage may at times be under revision with a high frequency—sometimes changing every few minutes. Please use your web browser's refresh or reload button (keyboard shortcut usually CONTROL + R) whenever you visit to ensure that you are seeing the latest version.
Graphic info for contacting me:
![]()
Last modified: Tuesday, January 19, 2010 21:27 -0500 (EST)
All Breakout™ puzzles, physics and math papers, and all other content of this website including the design of this website are the work of Diane G. Demers and are copyrighted (©) material: Copyright © 2002, 2005, 2009, 2010 Diane G. Demers. All rights reserved. The Breakout™ name and logo are trademarks (™) owned by Diane G. Demers.